Few weeks ago, a friend told me that you could easily guess the value of pi by (randomly) placing points on a surface, and see if they land inside a circle. I was bored today, so I decided to give it a try, and it turned out to be reallly really easy.

A little bit of theory

(Don't worry, this is basic math).

The problem

Imagine a square of height L, and inside of it, a circle of diameter L:

Now, If I throw some rocks inside of the square, how often will they land inside the circle ? (assuming I'm throwing those rock without aiming)

The answer it straight forward, It depends of the ratio of both the square's area, and the circle's area.

probabily of landing in the circle = square area / circle area

Which, in math, is expressed like this:

P(inside) = L²/(π x (L/2)²)

And can be simplified like this:

P(inside) = 4 / π

Which means we can express π using P(inside):

π = 4 x P(inside)

Finding P(inside)

Can we empirically find the probality ? Yes, just by throwing a lot of rocks inside the square, and counting the proportion of them that actually land inside the circle. The more rocks we throw, the closest we getto the real value of PI.

The thing is, we can easily simulate this, by using the random functions provided by our beloved computers. So basically, we can ramdomly generate points coordinates, and see if they "land" inside the circle.

How ?

This is quite simple, we can compute the distance between the center of the circle and a ramdomly placed point, if this distance is greater than the radius of the circle, then the point is not inside the circle.

Let's try

I've build a very simple python script for this :

from random import random

throw_counter = 0
landed_inside = 0

# Try to guess PI FOREVER !
while True:
    # generate random Coordinate inside a square (size 2 x 2)
    X, Y = random() * 2, random() * 2

    # Check if the point is inside a Cicle or diameter 2,
    # And origin (1, 1) 
    if ((X -1)**2 + (Y-1)**2) <= 1:
        # increase 
        landed_inside += 1
    throw_counter += 1

    # Each billion try, guess the value of PI
    if throw_counter % 1000000 == 0:
        pi = 4 * landed_inside / throw_counter
        print('Pi is approx %f' % (pi))

Let's run it :

groogroot@laptop $ python3 ./guess_pi.py

Pi is approx 3.134831

[...]

Pi is approx 3.141535

Pi is approx 3.141535

3.145335 is close enough for me: It works !!!

And of course, to get a better approximation of pi, we need to get a good approximation of P(inside), thus we need to test as much points as possible. In the following plot, we can see that the more attempt the script has made, the closer it was to the real value of pi (the orange line):

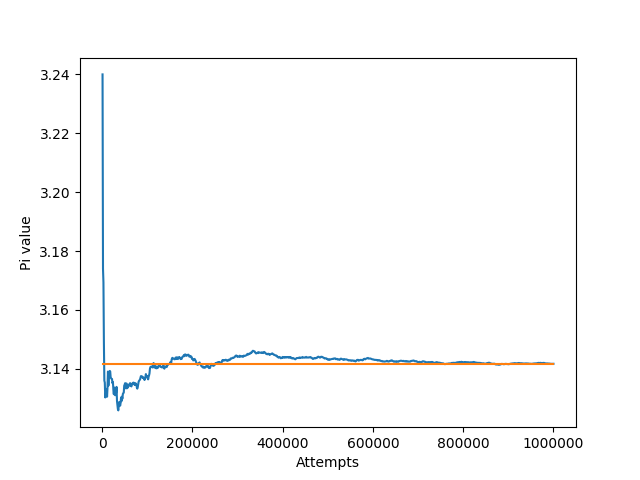
So it seems possible (for me) to get a good precision of pi using this really simple method, and I think this is kinda cool ! (in a nerdy way).

Conclusion

This was really easy ! It took me 5 minutes to plan, 5 minutes to code, and BAAM it worked ! Of course this could be improved in many ways, but those results are fine for me. :)

I had no idea this could be so easy !